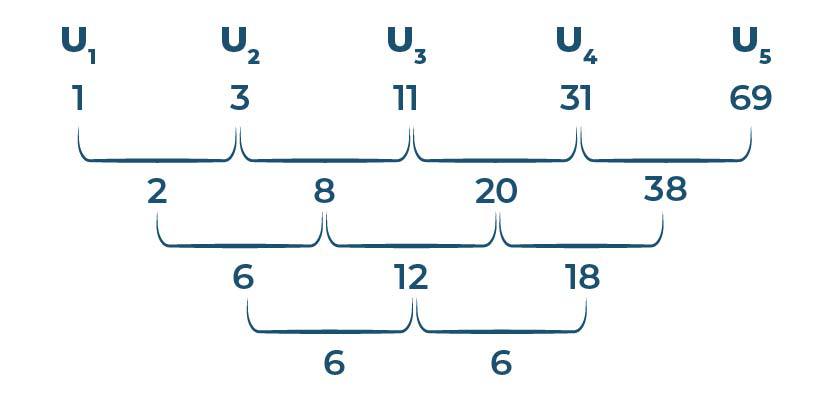
Rumus Aritmatika Bertingkat: Cara Mudah Menghitung Nilai Kumpulan Data
Pendahuluan
Rumus aritmatika bertingkat adalah salah satu cara mudah untuk menghitung nilai kumpulan data yang disusun secara bertingkat atau berjenjang. Dalam artikel ini, kita akan membahas tentang rumus aritmatika bertingkat secara lengkap dan mudah dipahami.
Table of Contents
Apa itu rumus aritmatika bertingkat?
Rumus aritmatika bertingkat adalah rumus matematika yang digunakan untuk menghitung nilai rata-rata dari sejumlah data yang disusun secara bertingkat atau berjenjang. Rumus ini sangat berguna untuk menghitung nilai-nilai statistik seperti rata-rata, median, dan modus dari sejumlah data yang disusun dalam bentuk tabel frekuensi.
Cara menghitung rumus aritmatika bertingkat
Untuk menghitung rumus aritmatika bertingkat, kita perlu mengikuti langkah-langkah berikut:
Hitung nilai tengah dari setiap kelas atau interval data.
Hitung frekuensi relatif dari setiap kelas atau interval data.
Kalikan nilai tengah dari setiap kelas dengan frekuensi relatifnya.
Jumlahkan hasil perkalian dari setiap kelas.
Bagi hasil penjumlahan dengan jumlah total frekuensi.
Contoh penghitungan rumus aritmatika bertingkat
Mari kita lihat contoh penghitungan rumus aritmatika bertingkat menggunakan data berikut:
| Kelas | Frekuensi |
|---|---|
| 10-20 | 5 |
| 20-30 | 8 |
| 30-40 | 12 |
| 40-50 | 10 |
| 50-60 | 5 |
Hitung nilai tengah dari setiap kelas.
- Nilai tengah kelas 10-20 = (10 + 20) / 2 = 15
- Nilai tengah kelas 20-30 = (20 + 30) / 2 = 25
- Nilai tengah kelas 30-40 = (30 + 40) / 2 = 35
- Nilai tengah kelas 40-50 = (40 + 50) / 2 = 45
- Nilai tengah kelas 50-60 = (50 + 60) / 2 = 55
Hitung frekuensi relatif dari setiap kelas.
- Frekuensi relatif kelas 10-20 = 5 / 40 = 0.125
- Frekuensi relatif kelas 20-30 = 8 / 40 = 0.2
- Frekuensi relatif kelas 30-40 = 12 / 40 = 0.3
- Frekuensi relatif kelas 40-50 = 10 / 40 = 0.25
- Frekuensi relatif kelas 50-60 = 5 / 40 = 0.125
Kalikan nilai tengah dari setiap kelas dengan frekuensi relatifnya.
- Nilai tengah kelas 10-20 x frekuensi relatif kelas 10-20 = 15 x 0.125 = 1.875
- Nilai tengah kelas 20-30 x frekuensi relatif kelas 20-30 = 25 x 0.2 = 5
- Nilai tengah kelas 30-40 x frekuensi relatif kelas 30-40 = 35 x 0.3 = 10.5
- Nilai tengah kelas 40-50 x frekuensi relatif kelas 40-50 = 45 x 0.25 = 11.25
- Nilai tengah kelas 50-60 x frekuensi relatif kelas 50-60 = 55 x 0.125 = 6.875
Jumlahkan hasil perkalian dari setiap kelas.
- Hasil perkalian kelas 10-20 = 1.875
- Hasil perkalian kelas 20-30 = 5
- Hasil perkalian kelas 30-40 = 10.5
- Hasil perkalian kelas 40-50 = 11.25
- Hasil perkalian kelas 50-60 = 6.875
- Jumlah total = 35.5
Bagi hasil penjumlahan dengan jumlah total frekuensi.
- Nilai rata-rata = 35.5 / 40 = 0.8875
Jadi, nilai rata-rata dari data di atas adalah 0.8875.
Kesimpulan
Rumus aritmatika bertingkat adalah cara mudah untuk menghitung nilai kumpulan data yang disusun secara bertingkat atau berjenjang. Dengan mengikuti langkah-langkah yang tepat, kita dapat menghitung nilai rata-rata, median, dan modus dari sejumlah data dengan mudah.
FAQ
Apa itu rumus aritmatika bertingkat?
- Rumus aritmatika bertingkat adalah rumus matematika yang digunakan untuk menghitung nilai rata-rata dari sejumlah data yang disusun secara bertingkat atau berjenjang.
Bagaimana cara menghitung rumus aritmatika bertingkat?
- Untuk menghitung rumus aritmatika bertingkat, kita perlu mengikuti langkah-langkah berikut: hitung nilai tengah dari setiap kelas, hitung frekuensi relatif dari setiap kelas, kalikan nilai tengah dari setiap kelas dengan frekuensi relatifnya, jumlahkan hasil perkalian dari setiap kelas, dan bagi hasil penjumlahan dengan jumlah total frekuensi.
Apa manfaat dari rumus aritmatika bertingkat?
- Rumus aritmatika bertingkat sangat berguna untuk menghitung nilai-nilai statistik seperti rata-rata, median, dan modus dari sejumlah data yang disusun dalam bentuk tabel frekuensi.
Apakah rumus aritmatika bertingkat hanya bisa digunakan untuk data yang disusun secara bertingkat?
- Ya, rumus aritmatika bertingkat hanya bisa digunakan untuk data yang disusun secara bertingkat atau berjenjang.
Apa yang harus dilakukan jika terdapat nilai yang tidak termasuk dalam kelas atau interval data?
- Jika terdapat nilai yang tidak termasuk dalam kelas atau interval data, nilai tersebut harus dihapus atau dimasukkan ke dalam kelas atau interval yang sesuai.
Baca artikel lainnya di Google News